On considère le programme de calcul ci-dessous dans lequel x, Étape 1, Étape 2 et Résultat sont quatre variables.
Question⚓
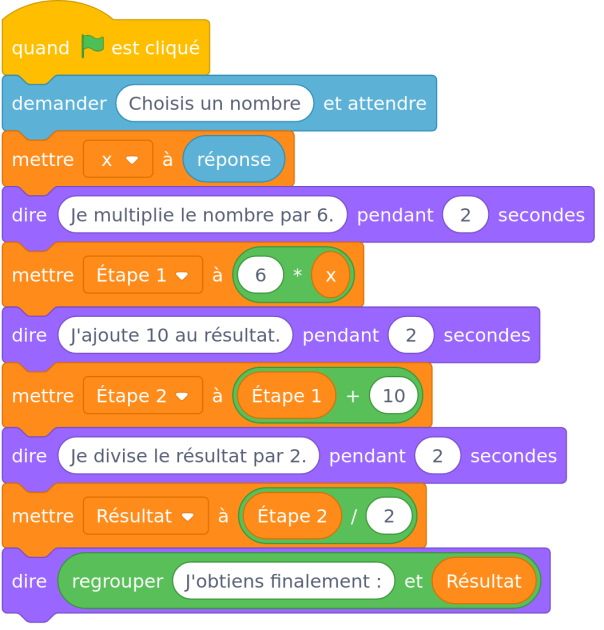
Julie a fait fonctionner ce programme en choisissant le nombre 5. Vérifier que ce qui est dit à la fin est : « J'obtiens finalement : 20 »
.
Solution⚓
D'après le programme le nombre 5 va être multiplié par 6 ce qui donne 30. Ensuite 30 va être additionné à 10, ce qui donne 40. Enfin, 40 sera divisé par 2 ce qui donne 20.
Le programme affichera ensuite le texte associé à la valeur de la variable «Résultat» qui vaut 20 ce qui donnera l'affichage suivant : « J'obtiens finalement : 20 »
.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Question⚓
Si l'on appelle \(x\) le nombre choisi au départ, écrire en fonction de l'\(x\) l'expression obtenue à la fin du programme, puis réduire cette expression autant que possible.
Solution⚓
L'expression est :
\(\frac{6x + 10}{2}\)
ce qui équivaut à (réduction de l'équation) :
\(\frac{6x}{2} + \frac{10}{2}\)
\(\frac{6}{2}\times x+ \frac{10}{2}\)
\(3x + 5\)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Question⚓
Maxime utilise le programme de calcul ci-dessous :
Choisir un nombre
Lui ajouter 2
Multiplier le résultat par 5
Peut-on choisir un nombre pour lequel le résultat obtenu par Maxime est le même que celui obtenu par Julie ?
Solution⚓
L'expression mathématique du résultat obtenu par le programme de Maxime est : \((x+2)\times 5\)
Pour trouver un nombre qui donne le même résultat qu'avec le programme de Julie il faudrait que ce nombre \(x\) réponde à l'équation \((x+2)\times 5=3x + 5\)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Résoudre une équation à une inconnue :
\((x+2)\times 5=3x + 5\)
\(5x + 10=3x + 5\)
\(5x - 3x = 5 - 10\)
\(2x = -5\)
\(x = - \frac{5}{2}\)
\(x=-2,5\)
Le nombre qui donne le même résultat que ce soit dans le programme de Maxime que dans le programme de Julie est \(x=-2,5\)
Effectivement, si nous vérifions :
programme de Julie : \(3x + 5\) avec \(x = -2,5\) cela donne
\(3\times (-2,5)+5= -7,5 + 5\)
\(3\times (-2,5)+5= -2,5\)
programme de Maxime : \((x+2)\times 5\) avec \(x = -2,5\) cela donne
\((-2,5+2)\times 5= -0,5\times 5\)
\((-2,5+2)\times 5=-2,5\)
Il s'avère donc que le nombre \(-2,5\) donne, non seulement le même résultat dans les deux programmes mais, également, redonne exactement le même nombre en sortie que celui qui a été donné en entrée soit \(-2,5\).